Main page
About us
Sliding Bearings Consulting
Advertising Opportunities
to Metals
to Fundamentals of metals
Dr. Dmitri Kopeliovich
Most of the processes in metals and alloys proceed by means diffusion and self-diffusion.
Diffusion in alloy is a process of transfer of atoms of different alloy components, resulting in changing chemical composition of some of the alloy regions.
Self-diffusion is a process of transfer of atoms of a certain element among themselves.
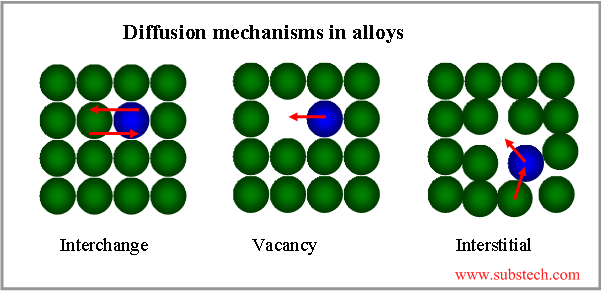
Diffusion mechanism is determined by the energy barrier that an atom must overcome in order to change its location. Some diffusion (self-diffusion) mechanisms are presented in the picture.
Metallic atoms diffuse mostly by the vacancy mechanism and elements with small atom sizes (H, N, C) diffuse by the interstitial mechanism.
Besides diffusion within the crystal, grain boundary (surface) diffusion may occur. As the grain boundaries regions are saturated with crystal lattice imperfections, energy barrier (activation energy) here is relatively low, therefore the diffusion rate along these regions is much higher, than the volume diffusion rate.
The classical laws, describing the diffusion process, are Fick’s laws:
First Fick’s law is used for diffusion in steady state (concentration gradient of the diffusing element does not change in time).
First Fick’s law states:
J = - D ( ∂C/∂x )
Where
J – diffusion flux (quantity of material that crosses a plane of unit area perpendicular to the diffusion direction for time unit), mol/ (length2 *time);
D – diffusion coefficient or diffusivity of the material, length2/time ;
∂C/∂x – concentration gradient in the diffusion direction, mol/(length3 *length).
to top
Second Fick’s law is used for transient (not steady state) diffusion process.
Second Fick’s law states:
∂C/∂t=D(∂2C/∂x2)
Where
∂C/∂x – concentration gradient in the diffusion direction, mol/(length3 *length);
D – diffusion coefficient or diffusivity of the material, length2/time ;
C – concentration of the diffusing material, mol/length3
The diffusion coefficient is not a constant. It is a function of crystal structure, temperature and material concentration.
The temperature function is expressed by the following equation:
D = D0e-Q/RT
Where
D - the diffusion coefficient, length2/time;
D0 - the maximum diffusion coefficient, length2/time;
Q -activation energy for diffusion, energy/mol;
T - absolute temperature, Kelvin;
R - gas constant, energy/(temperature*mol).
to top
